But what is interpolation? Basically it involves two constant values, a and b, and finding values that fall in between this range. Here is a common lerp() algorithm you'd find in most languages.
proc/lerp(a, b, t)
return a+(b-a)*t
The parameter t represents a value between 0 and 1. The value 0 is the 'start', and 1 is the 'end', everything else is in between. So if t=0.5, then you would be given the approximate midpoint between the two values.
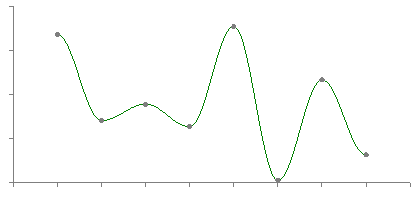
However, if you wanted a more smooth function than a linear graph, that is, a function that is twice or more differentiable, you could use a cosine function! This is what is known as cosine interpolation (or, alternatively, trigonometric interpolation)
var/pi = 3.141592653
proc/cerp(a, b, t)
var/f = (1-cos(t*pi)) * 0.5
return a*(1-f)+b*f
t in this proc functions identical to the previous. This would give you a graph that looks a lot smoother than a linear one, if you wanted a natural acceleration toward an endpoint. Take a look at the differences yourself:
Linear:
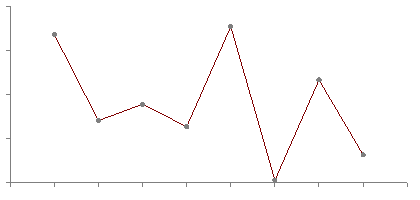
Cosine:
Now, just why would you use this? Say you knew what amount of experience you needed for level 1 (50 exp) and level 100 (10,000 exp). In order to find the values in between you'd need to do a lot of number crunching, or manually define all the levels yourself. That's terrible, though! The alternative is far cleaner and faster:
var/exp_to_lvl1 = 50
var/exp_to_lvl100 = 10000
proc/determine_exp(level)
var/coefficient = level/100 // this is essentially the t value from the interpolation methods
// Now you can do lerp()
return lerp(exp_to_lvl1, exp_to_lvl100, coefficient)
// Or cerp()!
return cerp(exp_to_lvl1, exp_to_lvl100, coefficient)
Hooray! Math makes things easier!
EDIT: Some minor corrections to some of the formulas I posted.